
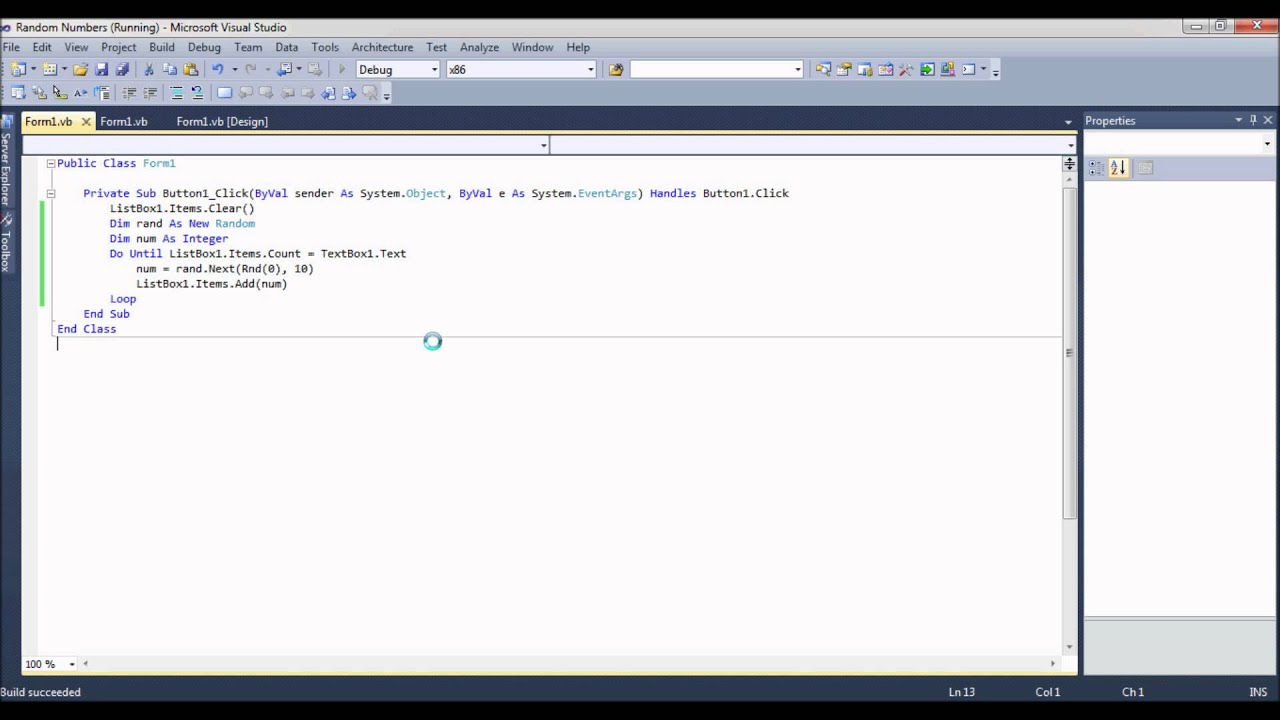
Life insurance, whole life policy, level annual benefit premiums, benefit reserves. Poisson distributions, random variables, variances, compound distributions, independent processes. Random variables, gamma distributions, variances, means, Poisson distributions, expected values, negative binomial distributions. Term insurance, benefits, premiums, loss random variable.
Survival function, de Moivre's law, limiting age, integrals. It deals with the following topics from the SOA and CAS syllabus: Q1 The sample examination consists of forty multiple-choice questions. Common sense, however, suggests that the stopping rule should not have such an arbitrary influence on the answer, and that we should continue to scale (55) by n − 1 2 - even though the ‘sample size’ n is data-dependent. If we did so, the reference posterior odds would be multiplied by θ ˆ 1 2 = 0.707, leading to a value of 4.21, corresponding to (slightly) weaker evidence against ESP. Slavish application of our general recommendations would appear to imply that we should scale (55) by r − 1 2 rather than n − 1 22 as in §7.2, so renormalising it to a single observation which is, however, now geometric rather than Bernoulli. There is, however, another, quite distinct problem that arises: how should we specify the appropriate scaling factor under M 1 ? After all, we now have observed, not n independent Bernoulli trials, but r independent geometric trials.
(However, because (55) is not normalisable, there is now no corresponding proper "reference prior structure".) We see then that the well-known dependence of the Jeffreys prior on the stopping rule, which might seem prima facie to be problematic, is of no essential practical importance in our approach. (This is a general feature, at least for exponential families: the Fisher information evaluated at the ma X 1mum likelihood estimate is always the same as the observed information, and this latter is not affected by the stopping rule.) Consequently the integral in (41) is effectively unchanged - in fact, the reference odds, calculated exactly as in (53), is now 5.951. (55) d μ 1 * ( θ ) = r 1 2 θ − 1 ( 1 − θ ) − 1 2Īlthough (55) differs from (51), we see that they are essentially identical in the region of θ = θ, i.e. When the number of those values less than p first reaches n, the number of values that are greater than p is a draw from the negative binomial distribution. Another way is to generate a sequence of U(0, 1) random variable values. If p is small, it is possible to generate a negative binomial random number by adding up n geometric random numbers.

The maximum likelihood estimate of p from a sample from the negative binomial distribution is n n + x ¯ ’, where x ¯ is the sample mean. The mean and variance of a negative binomial distribution are n 1 − p p and n 1 − p p 2. The PMF of the distribution is given by P ( X − x ) = ( n + x − 1 n − 1 ) p n ( 1 − p ) x. The number of failures before the nth success in a sequence of draws of Bernoulli random variables, where the success probability is p in each draw, is a negative binomial random variable. Sinharay, in International Encyclopedia of Education (Third Edition), 2010 Negative Binomial DistributionĪs mentioned earlier, a negative binomial distribution is the distribution of the sum of independent geometric random variables.


 0 kommentar(er)
0 kommentar(er)
